October 25, 2018 k-2-math-practices, 6-8-math-practices, 3-5-math-practices, mp-using-tools
Three Ways to Use Appropriate Tools Strategically (Mathematical Practice 5)
By: Jeff Todd
There is a great deal to say about how to use appropriate tools strategically, which is Mathematical Practice 5 from the Common Core State Standards. It is simple to say that this standard is about using a compass, protractor, ruler, or similar physical tool. There is so much more to using tools than just the use of physical objects. As I read in an article recently, even extremely simple tools are the product of a long period of experimentation, experience, observation, reflection, and recollection. This is the focus on tools I will address in this post.

Tools fall into three broad categories: physical tools, cognitive tools, and software tools. The download for this post is a tip sheet with examples of tools you can put into practice to teach certain topics at each grade level. If you are interested in the other Standards for Mathematical Practice, please see my previous posts on Standards 1 through 4.
To assist teachers in the Mathematical Practice 5, I've created a tip sheet with examples of tools you can put into practice. This tip sheet outlines choices you can use for teaching students to use appropriate tools strategically in each strand, at each grade level span. By giving students choices and talking with them about why they chose a specific tool, you can help them grow in their choice of strategies.
Using Physical Tools Strategically in Mathematics
I use many tools in my classroom, but the focus of this standard is not only to have students use tools, but also to encourage them to choose between tools, and to discuss why they might use them. This is the objective behind the Standards for Mathematical Practice, developing in students the ability to reason — which, in this case, is about using tools to investigate and solve problems.
This post includes a few examples of how to give students a choice of tools, but if you are looking for a more complete list of physical tools and manipulatives, be sure to download the related teacher tip sheet.
One way to help students to use appropriate tools is by teaching them about geometric transformations. I work with students on using different tools to experiment and to solve problems with transformations: transparencies or tracing paper to copy figures, cardstock to cut out figures, coordinate grids for graphing figures, or, if I am feeling brave, a compass and a straightedge with a blank sheet of paper to redraw figures. It is an investment of time to teach students to use these tools, but as a result when students are faced with new problems, they will have a wealth of tools to use. In addition, we can have rich personal and classroom discussions about how to use appropriate tools strategically.
An example from the elementary grades could be when students need to estimate the sum of two-digit numbers. Some tools that might be available in this case are number lines, hundreds grids, paper and pencil, various types of counters, and perhaps a calculator. These objects are all valid tools. Giving students a choice of materials and having discussions with them about their choices will lead them to use appropriate tools strategically.
Recommended resources:
|
Teddy Bear Counters |
Fall Leaf STEAM Lesson |
3 Little Pigs STEAM Lesson |
Using Cognitive Tools Strategically in Mathematics
Just prior to the turn of the 20th Century, many German and Russian philosophers related the use of tools to human and social development; I loved learning about them in graduate school. Many educators study Vygotsky, whose developmental psychological theories are rooted in a paradigm of tool use. There are many cognitive tools that we can teach our students to use. One of my favorite new cognitive tools will give you an idea of why they are important, and how they can be used in the classroom.
A few of my recent posts are about using number bonds, which is a cognitive tool or representation that helps students to understand the relationship of parts and wholes through the operations of addition and subtraction. Here is an example of a number bond used for fractions. Notice how students can write four different equations related to the number bond.
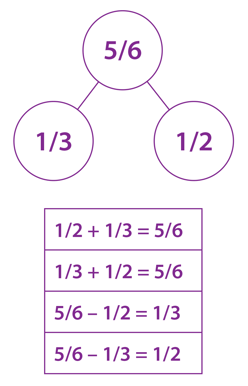
A number bond is a durable mental model or tool that can be used with students and revisited through the elementary and middle school curriculum. It can be used with whole numbers, fractions, decimals, integers, and rational numbers. Students can apply this tool is to organize information from word problems and to form an equation to solve the problem. This is just one way that students can use appropriate tools strategically — even when the tools are cognitive in nature.
Recommended resources:
|
Ten-Frame Activities |
Add Fractions with Like Denominators |
Math Instructional Strategies |
Using Software Tools Strategically in Mathematics
Finally, students can use appropriate tools strategically through technology. They can use scientific calculators, graphing calculators, spreadsheets, and an endless supply of online applications to help them solve problems. There are a few websites and free apps that I find extremely helpful in my classroom.
The first website is The National Library of Virtual Manipulatives, which is easy to locate via a web search. I like these tools because I can use them for demonstration, or, if I have computers available, I can set students up to explore or complete a lesson on their own. The site has virtual manipulatives for every topic, at every grade level.
The second is the Desmos graphing calculator, which is also available as a free app for Android or iPhones. It’s great to use in the classroom because the online calculator looks and functions just like the app on a tablet or phone. Because my school doesn’t have a strong technology infrastructure, I ask students to use their own devices, while I display how the calculator is used with my computer and a projector. Because the graphing calculator takes students’ minds off the task of graphing by hand, it possible for me to address some conceptual ideas more quickly and easily. Even I, the teacher, sometimes need to use appropriate tools strategically!
RELATED RESOURCES:
|
|
|
|
|
|




















