In this article, you'll discover how to help students develop an understanding of the relationship between addition and subtraction! These algebraic thinking worksheets will assist you with the primary goal of initiating algebraic thinking—the relationship between addition and subtraction—in the early grades.

Developing the Foundation for the Relationship Between Addition and Subtraction

While most of us first think of using “x” and “y” for algebra, in the early grades variables are not the focus. Nonetheless, thinking about unknown quantities is possible even for our youngest students. Problems such as “I have three fish and I want to have five. How many more do I need?” foster algebraic thinking in the early grades and foster the development of the relationship between addition and subtraction.

This idea of the inverse relationship between addition and subtraction, that one “undoes” the other, is the first of many inverse relationships that students will encounter. A solid foundation in the relationship between addition and subtraction will serve students well in the future as they learn about other inverse relationships. Therefore, developing the foundation for the relationship between addition and subtraction is critical for young students!

Representations That Show the Relationship Between Addition and Subtraction

As in most learning about math, the use of representations will help students grapple with relationships between numbers. The two representations that I believe work best and have used the most for algebraic thinking in Grade 1 are number bonds and tape diagrams.

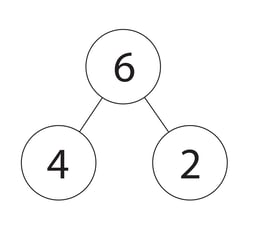
You may have seen previous posts on number bonds, so I won’t go into detail here, except to show an example. The number bond below shows the relationship for addition and subtraction between 2, 4, and 6. From it, we can write the fact family of relationships between these numbers: 2 + 4 = 6, 4 + 2 = 6, 6 – 2 = 4, and 6 – 4 = 2.

Similarly, this relationship can be shown using a tape diagram, as in the example below.

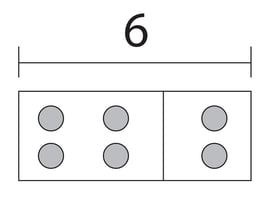
Context is critical to students understanding and developing representations. When using the above representations, it is important that students understand from the context of the problem what the total is and what the parts are. In both the number bond and the tape diagram representations, the total is placed above the parts.

I would definitely introduce these representations after students have had some experience with missing part problems using counters or other manipulatives. After they have had the chance to use manipulatives for a concrete experience, the number bonds and/or tape diagrams can then be used as semi-concrete representations that move students to create mental models of their concrete experiences.

Algebraic Thinking Worksheets for Grade 1

Today I have three algebraic thinking activities available for download!

The first worksheets focus on using related addition and subtraction facts to subtract. With the second algebraic thinking worksheets, students will use models to solve subtraction problems with unknowns. The final activity worksheets focus on using models to solve addition problems with unknowns! Each of the algebraic thinking activities includes the answer keys.

One benefit of the downloads that accompany this post is that they provide practice for unknown parts and unknown whole types of problems. Below is one of the sheets included in my bundle of algebraic thinking worksheets!