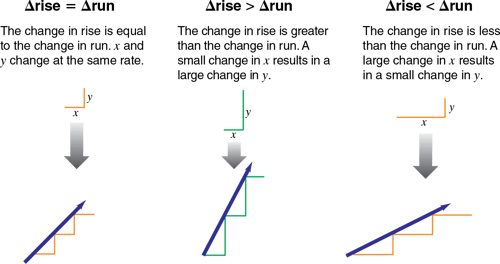
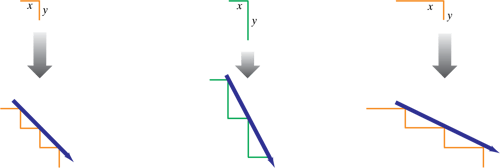
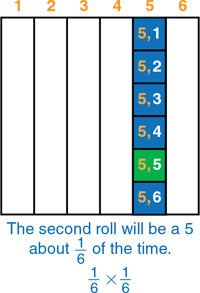
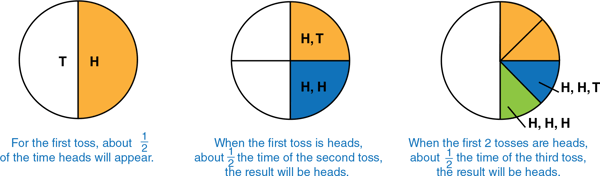
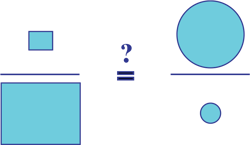
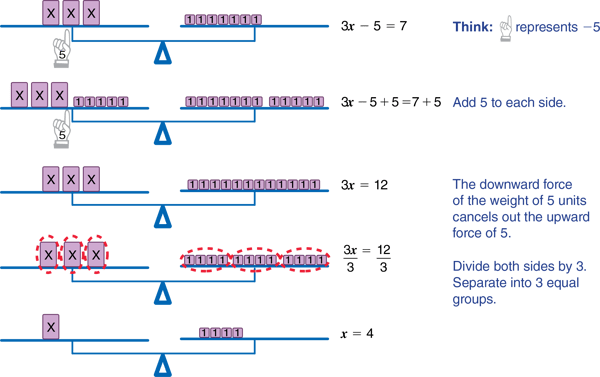
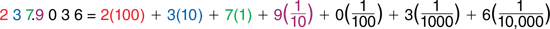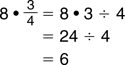1.800.221.5175
Mathematics
Sadlier PreK with Wiley Blevins
Knowledge-Building Early Childhood Program
Preview
|
Progress Mathematics
Grades K–8
Reading & Writing
From Phonics to Reading
Grades K–3
Building Reading Success with Wiley Blevins
Grades K–5
Vocabulary
Vocabulary Workshop, Tools for Comprehension
Grades 1–5
Vocabulary Workshop Achieve
Grades 6–12+
|