Math problem solving strategies should begin as early as Kindergarten or Grade One! As nonfiction reading has seen a stronger emphasis in recent years, we can think of word problems as part of the genre of nonfiction. The downloads for today’s post include several templates or graphic organizers to help students make the connection between word problems and equations that represent those problems.

As a math teacher, I have heard many times that “we are all teachers of reading,” and this post will show how the two areas relate, both math and reading, as students create representations to help them move from words to equation and vice versa. Plus, grab my downloadable templates for multiple representations below! By using these templates to design lessons, you are able to address many of the Standards for Mathematical Practice that undergird math word problem solving strategies.

• SMP 1: Make sense of problems and persevere in solving them
• SMP 2: Reason abstractly and quantitatively
• SMP 4: Model with mathematics
• SMP 7: Look for and make use of structure

Manipulative and visual representation of math word problems are closely related. These representations are the math problem solving strategies that students can employ. I hope you’ll bear with me as I give a bit of the history of what I have learned about teaching students using manipulatives and representations. In the 1960s, Jerome Bruner coined the terms enactive, iconic, and symbolic to describe how students progress from using manipulatives, to making drawings based on the manipulatives, to using numbers and symbols alone. Today, we might call these steps concrete, representational (semi-concrete), and abstract. Singapore Math uses the terms concrete, pictorial, and abstract. These three sets of terms all refer to the same core strategy of using manipulatives with mastery to show a mathematical idea, then having students represent that idea using paper and pencil (re-presenting it), and, finally, using only numbers and symbols to represent it.

I would encourage you to have students first work with manipulatives such as teddy bear counters, little cubes, or even beans. These help to show the relationships between the situation students are reading about in a word problem. It is best to have them use the template to represent their idea using a ten frame, number bond, array or area model, and tape diagram (semi-concrete, pictorial or iconic representations). Finally, they will understand the meaning of the equation (abstract or symbolic representation) when they write it.

Math Word Problem Solving Strategies for Students

If you are looking for math word problem strategies in Kindergarten through Grade 4, you will find the downloadable templates below very helpful. By using the templates, you can give students strategies to read word problems and create representations to solve them, or even give them a representation and have them create word problems. Use these downloadable templates to give students math problem solving strategies involving addition, subtraction, multiplication, and division. Print them and use them today in your class!

Kindergarten and Grade 1—Adding

In the earliest grades, students are only expected to add. A typical word problem might be, “Chris has three oranges and two apples. How many pieces of fruit does Chris have all together?” Students can model the problem using cubes of different colors. The downloadable template has a spot for the question, then students can make a drawing based on their manipulatives. The key semi-abstract representations for these students are ten frames and number bonds. Particularly with number bonds, students are having to think about parts and totals. Finally, students write an addition sentence.

There are two templates available for adding. The first has one ten frame targeted for Kindergarten where students only add within ten. The second has two ten frames targeting first grade, where students add within twenty. Advanced students could be pushed to represent their addition sentences using a number line, but that is not included with this download.

Grades 1 and 2—Adding & Subtracting

As students progress through Grade 1 and into Grade 2, they are learning about the relationship between addition and subtraction. Conceptually, this is different from early work with just adding. Strategies for solving addition word problems with two addends can be formulaic. The two numbers in the word problem must be added, but when students encounter word problems with a missing part, they must have strategies and representations to think about parts and wholes.

On the template for adding and subtracting, you will find number bonds and a tape diagram. Each template has a frame with two number bonds, one with the “whole” x-ed out, the other with one of the “parts” x-ed out. Students need to read the problem and decide whether it is a missing-part or a missing-whole type problem. This is where we need to tie in the reading with the math. Similarly, students should complete the tape diagram using the part and whole ideas, but this time using a “?” or a letter as a variable to represent the unknown.

Finally, students should write at least one addition or subtraction sentence to represent the problem using a “?” or variable for the unknown. Then, they can write the number sentence showing the “solution” in place of the question mark or variable. Advanced students could be pushed to represent their number sentence using a number line, but that is not included with this download.

Grade 3 and 4—Multiplying & Dividing

Building on work in second grade, Grade 3 and Grade 4 students need to adopt strategies for solving word problems that involve multiplication and division. These problems require different representations than the strategies for math word problems involving addition and subtraction.

The downloadable template for Grades 3 and 4 include a space for an array model, an area model and a tape diagram. Just to be clear, students can represent multiplication and division word problems using any of these three representations:

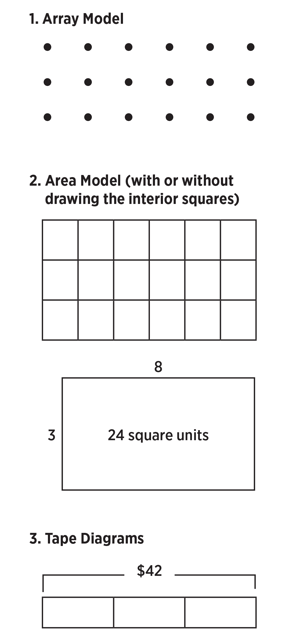
You can see that this series of abstract representations of multiplication and division move from the more concrete (semi-abstract) versions where you can count dots or squares, to more abstract versions where students move away from counting to finding solutions. This also aids students in the beginning use of variables to represent unknowns, as they can label missing parts of the area or array models with a letter.

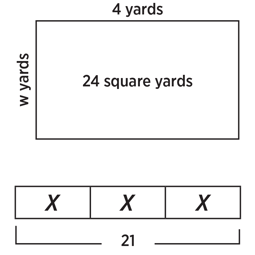
In the last box of the downloadable template, students are asked to write the equation using a variable or question mark for the unknown and then to “solve” it. By solving, I mean not using algebraic steps (i.e., divide both sides by three), but instead just to write “x = 7” in the case of the example immediately above. Students could use any form of reasoning, including going back to using physical counters and dividing them into equal groups.

How The Standards For Math Practice Relate To Using The Templates

I want to share some thoughts about how these downloadable templates can be used to develop students’ strategies to solve math word problems and tap into the Standards for Mathematical Practice (SMPs).

SMP 1: Make sense of problems and persevere in solving them.

When students are asked to make a diagram, they must be clear about what parts and wholes are. Giving them representations such as number bonds, area and array models, or tape diagrams helps them make sense of the problems and the relationships of the elements that they find when reading the word problem.

SMP 2: Reason abstractly and quantitatively.

When students create a representation such as in Download 4, (3 boxes of “x” equal to 21), this is an abstract representation. It doesn’t say anything about what the problem is about. When students read a word problem involving quantities (three toys that cost $21 total) and make the tape diagram they move from quantities to abstractions. Another way to use these templates is to complete the tape diagram (or array or area model) and ask students to fill in the other boxes. In other words, students will create their own word problems from the tape diagram. They start with the abstract representation and come up with a quantitative idea (this problem could be 21 apples and three people or 21 chocolates and three boxes, etc).

SMP 4: Model with mathematics.

These kinds of models, such as area models and tape diagrams, if introduced early, will help students when they use area models in upper grades to model more complex problems.

SMP 7: Look for and make use of structure.

Reading word problems and then making representations using the templates will help students look for keywords and how they relate to the structure of parts and wholes, rows and columns, factors, totals, and divisors. Seeing the common underlying structures using number bonds, ten frames, area and array models, and tape diagrams helps to reinforce common underlying structures that appear in various word problems.

In Summary

Download and use my free templates to help students make connections between word problems and equations that represent those problems. When you do this, you will engage students in the use of the Standards for Mathematical Practice outlined above, giving them ways to picture word problems in their heads and create representations that show the relationships of the quantities involved.