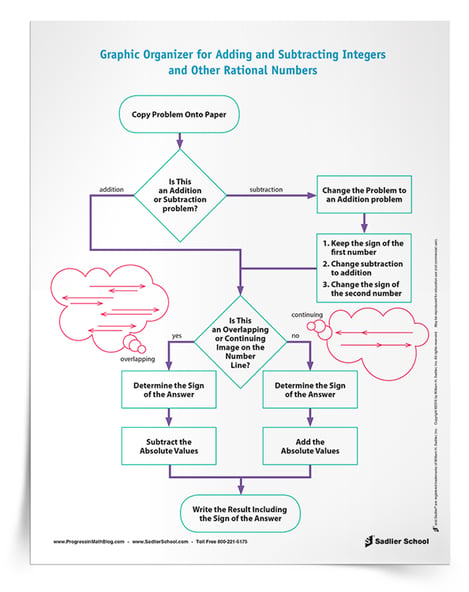
I have always found that teaching students about the addition and subtraction of integers and rational numbers is one of the most difficult math topics. It’s something that seems very confusing for them. This post discusses an approach to adding and subtracting integers and rational numbers that I have found to be most helpful for struggling students. The download for this post is a graphic organizer that students can follow in order to practice adding and subtracting integers and rational numbers. It is the kind of scaffolding that can help students to learn the thinking that is necessary to be successful at simplifying these expressions.

Adding Integers

Adding integers is the foundation upon which the addition and subtraction of rational numbers rests. Students need to have a solid understanding of adding integers in order to move on to subsequent topics. I have seen and have made the following mistake with my students: in the interest of “moving on” in the curriculum, I hope that my students will eventually understand adding integers. More than most other topics, it is critical that all students master this before moving on. Without being able to add integers, subtracting integers and operations with rational numbers will be confusing.

The most successful strategy for students is to visualize integer problems on a number line. I ask students to classify problems as overlapping or continuing by looking at the integer addition problem and visualizing it on a number line (after they have had plenty of practice creating them). Continuing problems are when two integers of the same sign are added, for instance -4 + -5 or 3 + 4. Number line diagrams for these expressions are two rays end to end. Overlapping integer addition problems are when a positive and a negative number are added, such as 2 + -3 or -6 + 5. The number line models that overlap have two rays that are pointing in opposite directions. See the examples below.

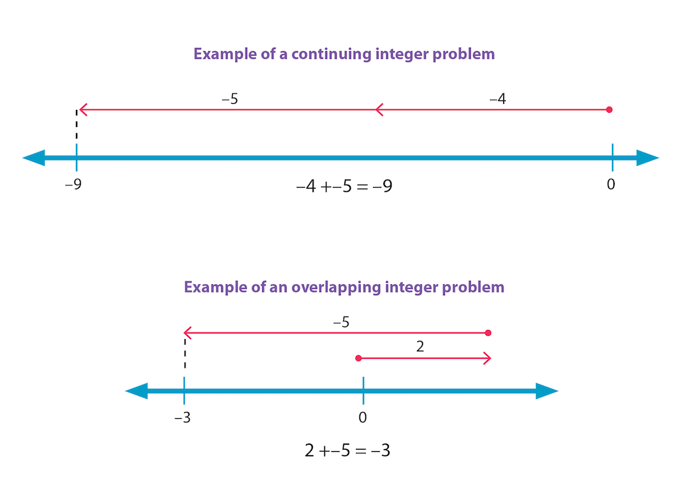
I find that students are able to easily state which of the two situations, continuing or overlapping, matches the sum at hand. Having the mental image in mind, they easily choose whether to add or subtract the absolute value of the addends. While verbal rules such as “when I add opposites I subtract” or “just add numbers when the signs are the same” may not always be clear to students, the mental number line representation of the sum is both durable and useful.

Once students establish whether the situation is overlapping or continuing, I ask them to determine the sign of the answer and write it down. Then I ask them to perform the correct operation on the absolute values of the two numbers. Once they can do this consistently and reliably, they are ready to move on to other topics.

I am aware that there are other methods you can use to teach, represent, and visualize adding integers. I like them and I use them to teach students. Nonetheless, when students are struggling, I find the above approach works the best.

Subtracting Integers

A mathematically robust and simple way to think about subtracting integers is to rewrite the subtraction as the addition of the opposite number. There are other ways that subtraction can and should be taught, but for students who are struggling, training them to rewrite the subtraction as addition of the opposite number is simple and reliable. I have often seen this process referred to as Keep/Change/Change. In other words, students 1) keep the first integer, 2) change the addition to subtraction, and 3) change the second integer to its opposite.

I have found that students can understand all of the pieces of this process, but it is still a challenge for them to put the pieces together in a multi-step process. That’s why I developed this graphic organizer for the addition and subtraction of integers and rational numbers. It helps students to keep track of where they are in the process and to be able to determine what they should do next. It is the kind of scaffolding that struggling students may need to be successful.

Adding and Subtracting Rational Numbers

Once students have mastered the addition of integers, then adding rational numbers becomes quite simple for them, assuming that they can accurately add and subtract fractions and decimals. The downloadable graphic organizer can be used for adding or subtracting any rational numbers.

The addition and subtraction of integers and rational numbers is one of the gateway foundational skills for high school math and beyond. As teachers, we should do our best to make sure that every student can add integers fluently before having them attempt subtraction of integers, and later adding and subtracting rational numbers. Using the downloadable graphic organizer will help your struggling students understand this key concept.