January 31, 2017 3-5-math-practices, mp-structure
How to Look for and Make Use of Structure in the Elementary Classroom: Math Standard 7
By: Jeff Todd
A topic that I have been thinking about recently is the use of area models to teach multiplication. Today’s post looks at how we can look for and make use of structure (Standard for Mathematical Practice 7). We will combine the topics of place value and area models in the elementary curriculum in order to help students see the structure of multi-digit multiplication. Today’s download will help your students see how the structure of the number system place value can be used to multiply two numbers. This method is a step in the process of the conceptual development of multiplication in Grade 4 that will help students eventually learn the standard algorithm for multiplying two two-digit numbers by the end of Grade 5.
If you are a math supervisor or instructional coach, or even a teacher from another grade, I hope that this post will help you see how students can look for and make use of structure at the elementary level. There are many other topics where you can apply Mathematical Practice 7, such as sorting shapes by their attributes, the commutative and associative properties of addition and multiplication, and writing number sentences from number bonds, for instance. Today, however, we will focus on place value and area models.
The topic of place value of whole numbers all on its own is a great place for students to look for and make use of structure. Digits in the tens place can and should be read using that structure. In the number 321, the digit “two” represents the number 20. Studying whole numbers in elementary school is where students first encounter this type of structure, which seems so natural to us.
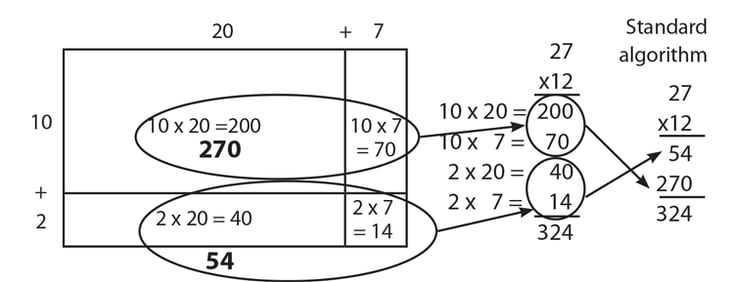
Assuming that students have prior knowledge of place value, we will use the problem 27 x 12 to illustrate how students can look for and make use of structure with an array model. The first task is to draw a divided rectangle where we can decompose 27 and 12 using place value.
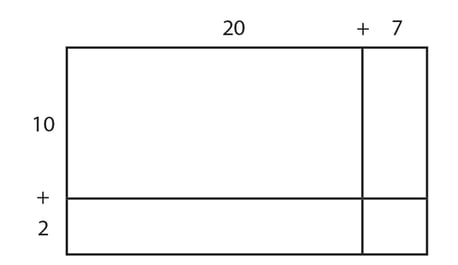
Students should look for and use the structure of place value to decompose the two numbers, 27 = 20 + 7 and 12 = 10 + 2. This structure is then used to label the sides of the rectangle.
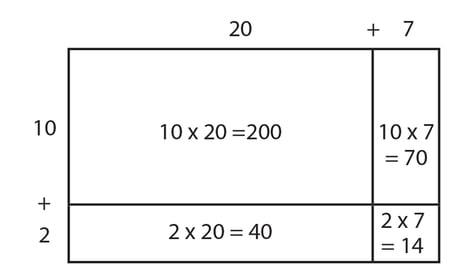
Students should then find the area of each box. This is called the method of partial products—finding several smaller products that are then added to calculate the final product for the given problem. In earlier grades, students have learned—by using smaller numbers—that multiplication is structured as a rectangular array. Students then apply this structure using larger numbers.
The next step is what teachers can sometimes miss, and which is so important, is relating the structure of the area model to the development of the standard multiplication algorithm. I like to have students create the sum by writing out the whole problem next to the area model.
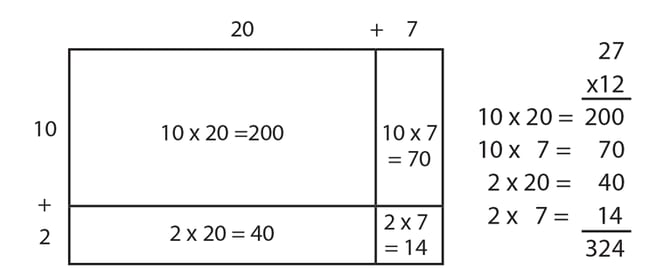
Students should be able to look for and make use of the structure of this problem and discuss it with each other in pairs and with the whole class. Students can explain how each number on the array model relates to the calculations on the right. They can notice that largest area comes from multiplying the numbers in the tens place, that the smallest number comes from multiplying the numbers in the one place, and that the other two areas are in between by multiplying numbers in the tens and ones place.
For teachers in Grade 5 when the standard algorithm is the goal, comparing this method with the standard algorithm allows students to look for and make use of structure and promotes a deeper understanding of the process of multi-digit multiplication. Thus, 200 and 70 from the area model add up to 270 in the standard algorithm. Similarly, 40 and the 14 from the area model become 54 in standard algorithm.
If you would like your students to look for and make use of structure, you can download today’s problem set (with answer key) and help your students understand how place value works when computing multi-digit multiplication.




